Equação Polinomial na Forma Fatorada
Funções Polinomiais
Quando estudamos o gráfico de uma função talvez a principal razão para isso, seja o de determinar o número e a localização (pelo menos aproximada) de seus zeros. Zero de uma função f é uma solução da equação.
Quando estudamos o gráfico de uma função talvez a principal razão para isso, seja o de determinar o número e a localização (pelo menos aproximada) de seus zeros. Zero de uma função f é uma solução da equação.
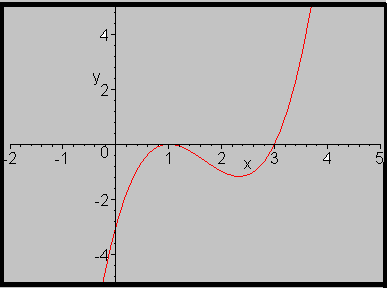
As raízes ou os zeros da função são todos os pontos do gráfico que cortam o eixo x do sistema cartesiano. No exemplo ao lado, temos os pontos x1=1 e x2=3 são considerados como as duas raízes reais deste gráfico da função ali associada.
Na antiga Babilônia, a fórmula para o cálculo das raízes exatas de uma equação geral do segundo grau foi muito discutida e estudada.
No século XVI, matemáticos italianos descobriram fórmulas para o cálculo de soluções exatas de equações polinomiais do terceiro e do quarto grau. Essas fórmulas são muito complicadas e por isso são raramente usadas nos dias de hoje.
Mas, como responder as seguintes perguntas:
Qual é o maior número de zeros que uma função polinomial pode ter?
Qual é o menor número de zeros que uma função polinomial pode ter?
Como podemos encontrar todos os zeros de um polinômio?
Este problema foi completamente resolvido pelos matemáticos até o início do século XIX.
No estudo das equações de primeiro e segundo grau é razoável supor que o número de raízes de um polinômio está relacionado ao seu grau.
Sabemos, por exemplo, que a equação x² = 0, tem uma única raiz igual a zero. Mas, na verdade, esta equação tem duas raízes idênticas, ambas iguais a zero.
Esta equação pode ser escrita como (x-0)(x-0)=0 . Esta forma (fatorada) de escrever a equação permite perceber, claramente, que a mesma possui duas raízes iguais a zero.
O mesmo se dá com a equação x² - 1=0 que apresenta duas raízes idênticas e iguais a 1.
Podemos encontrar facimente, muitos exemplos de equações de segundo grau que não têm nenhuma raiz real.
Considere, por exemplo, a equação x²+1=0 .
Ao tentarmos encontrar as raízes desta equação, chegaremos a x² = -1 , que não tem solução real. No entanto, se admitirmos que as raízes podem pertencer ao conjunto dos números complexos, esta equação tem duas raízes complexas conjugas, a saber, x1 = i e x2 = -i . Da mesma maneira que no exemplo anterior, esta equação pode ser escrita na forma fatorada como (x-i)(x+i)=0 .
No caso mais geral de uma equação de segundo grau, temos que a equação ax²+bx+c=0 pode sempre ser escrita na forma y = a (x - x1) (x - x2) , onde x1 e x2 são as duas raízes da equação, que como já vimos pelos exemplos acima, podem ser distintas, repetidas(iguais), ou mesmo complexas.
Este fato pode ser generalizado para equações polinomiais de qualquer grau. De um modo geral, sempre que x1 for um zero complexo de um polinômio P(x), isto é sempre que x1 for uma raiz complexa da equação P(x)=0 , temos que (x - x1) é um fator de P(x). Este fato foi estabelecido por René Descartes em seus estudos já publicados.
Definição: Toda equação P(x) = 0 de grau n >=1 admite ao menos uma raiz complexa.
Observação: Uma função polinomial de grau n tem, no máximo, n raízes reais distintas.
Observação: Uma função polinomial de grau n tem, no máximo, n raízes reais distintas.
Equação Polinomial na Forma Fatorada
Toda equação polinomial P(x)=0, então: an(x-r1)(x-r2)(x-r3) ... (x-rn)=0 é a forma fatorada dessa equação, onde r1, r2 ,r3, ..., rn são as raízes de P(x)=0
a) Fatore a equação: 2x² -3x +1=0
Então, chegamos às duas raízes x1 e x2 abaixo:
→ x1 = 3+1 / 4 →x1= 4/4 →x1 = 1
→ x2 = 3-1 / 4 →x2 = 2/4 → x2 = 1/2
→ x2 = 3-1 / 4 →x2 = 2/4 → x2 = 1/2
Logo, 2x² - 3x + 1=0, tem como forma fatorada a expressão:
2(x-1)(x-1/2) =0
b) Fatore a equação x³ - 2x² - x - 2 = 0 sabendo-se que 2, i, -i são as raízes dessa equação:
x³ - 2x² - x - 2 = (x-2)(x-i)(x+i) = 0
c) Fatore a equação x² - 8x +15 = 0
Passo1 -Achar as raízes da equação:
(usando Bhaskara) x= -(-8) ± √(-8²-4.1.15 /2.1 →x=8±√64-60 / 2
→x= 8±√4 /2 → x= 8±2 /2 →x1= 8 +2 /2 →x1= 10/2 →x1 = 5
x2= 8-2 /2 = 6/2 =3
Passo2: Então: x² - 8x +15 = (x-5)(x-3)=0
d) Escreva na forma fatorada a equação: 2x² - 32=0
Resolvendo a equação 2x² -32=0 (dividindo tudo por 2)→x²-16=0 → x² =16 →x=√16
→ x= ±4
Logo: 2x²-32 = 2(x+4)(x-4)=0
e) Decomponha num produto de fatores do 1º grau a equação x³ - 6x² +11x - 6 =0 sabendo que 1,2 e 3 são raízes dessa equação.
Solução: x³ - 6x² +11x - 6 = (x-1)(x-2)(x-3)=0
.........................................................................................................................................
Solução das 10 questões de Lógica e Matemática do post: Pegadinhas em Questões de Matemática.
1- (Esta pegadinha cai muito em concursos e vestibulares): Um determinado produto sofre um aumento de 10% no final de um mês e no final do mês seguinte ele sofre mais um aumento de 20%. Qual foi a porcentagem de aumento total que esse produto sofreu?
3- Se você está em uma corrida e passa a frente do segundo colocado, qual colocação você fica?
→x= 8±√4 /2 → x= 8±2 /2 →x1= 8 +2 /2 →x1= 10/2 →x1 = 5
x2= 8-2 /2 = 6/2 =3
Passo2: Então: x² - 8x +15 = (x-5)(x-3)=0
d) Escreva na forma fatorada a equação: 2x² - 32=0
Resolvendo a equação 2x² -32=0 (dividindo tudo por 2)→x²-16=0 → x² =16 →x=√16
→ x= ±4
Logo: 2x²-32 = 2(x+4)(x-4)=0
e) Decomponha num produto de fatores do 1º grau a equação x³ - 6x² +11x - 6 =0 sabendo que 1,2 e 3 são raízes dessa equação.
Solução: x³ - 6x² +11x - 6 = (x-1)(x-2)(x-3)=0
.........................................................................................................................................
Solução das 10 questões de Lógica e Matemática do post: Pegadinhas em Questões de Matemática.
1- (Esta pegadinha cai muito em concursos e vestibulares): Um determinado produto sofre um aumento de 10% no final de um mês e no final do mês seguinte ele sofre mais um aumento de 20%. Qual foi a porcentagem de aumento total que esse produto sofreu?
Solução: Se você pensou em somar 10% +20% e responder 30% você errou.
O jeito mais simples de calcular é tomar um valor fictício como 100,00 e fazer os cálculos ou seja: no final do 1º mês ele vai de 100,00 para 110,00 (100,00+10% de 100,00= 100,00 + 10,00) e no final do segundo mês você calcula 20% em cima do valor atualizado 110,00, que dá o total de 132,00 = 110,00 + 110,00.0,20 = 110,00 + 22,00. Veja então que o produto custará o valor atualizado com os dois aumento a importância de 132,00, que equivale a 32,00 de aumento ou 32% de aumento total.
2- Se um tijolo pesa um quilo mais meio tijolo, quanto pesa um tijolo e meio?
t = 1kg + t/2 → t - t/2 = 1kg → t/2 = 1kg → t=2 kg
1,5t = x →x = 1,5.2 = 3 kg
Resposta: 3 kg.
3- Se você está em uma corrida e passa a frente do segundo colocado, qual colocação você fica?
Fica como segundo colocado
4- Sabendo-se que 3 gatos matam 3 ratos em 3 minutos, quanto tempo levam 100 gatos para matar 100 ratos ?
Usamos uma regra de três composta:
3gatos..........3ratos..........3minutos
100gatos.......100ratos.......x
Note que gatos e minutos são grandezas inversamente proporcionais, então temos que inverter essa fração:
100/3 . 3/100 = 3/x → 1= 3x →x = 3
Logo, leva 3 minutos
5- Três garotos decidem atravessar um rio. O barco que pode levá-los, possui capacidade máxima de 150 quilos. Eles pesam: 50, 75 e 120 quilos. Como podem atravessar, sem afundar o barco?
Resposta: Vai 50 e 75, volta 50, vai 120, volta 75 e vai 50 e 75.
6- Complete a sequência corretamente:
Q, P, O N, M
Resposta L (letra anterior do alfabeto da sequência de letras)
7- Complete a sequência corretamente:
1,2,3,5,6,7,9,10,11;
Resposta: 13,14,15 (note que sempre pula um número após sequência de 3 números, então devemos pular o 12 os três números seguintes da sequência são: 13,14,15 )
8- Complete a sequência corretamente:
29,28,26,23,19;
Resposta: 14 (ver sequência, pula-se: 0, depois, 1, após pula 2, depois pula 3 e atual pula 4 números na sequência decrescente 18-17-16-15 e o que vem a seguir é o 14)
9- Complete corretamente a sequência:
88,84,76,60;
Resposta: 28 (sequência somando-se -4,-8-16 e atual -32→60-32=28)
10- Três amigos foram pagar uma conta de R$ 30,00 numa pizzaria. Cada um deu R$ 10,00 para a garçonete, totalizando os R$ 30,00 da conta. No caixa, verificou-se que a conta havia dado, na verdade, R$ 25,00. A garçonete devolveu o dinheiro aos três amigos, que decidiram ficar com R$ 1,00 cada um e dar os R$ 2,00 restantes de gorjeta para a garçonete.
Então, cada amigo pagou, portanto, R$ 9,00, totalizando R$ 27,00. Com os R$ 2,00 de gorjeta da garçonete, o total pago foi de R$ 29,00. Mas se eles haviam dado R$ 30,00 no início e não sobrou dinheiro algum, ONDE FOI PARAR O VALOR DE R$ 1,00 QUE COMPLETARIA OS R$ 30,00 DADOS PARA O PAGAMENTO?
Solução: Não podemos somar os 2,00 com 27,00 que foram gastos, pois ele já está incluso na conta, ou seja:
gastos: 25(conta)+2(gorjeta) =27
dinheiro arrecadado: 10+10+10 =30
troco: (30-27)= 3,00 (divididos 1,00 para cada um)
Conclusão: Logo a pizza custou R$25,00 + R$2,00 (Gorjeta) + R$3,00 (Troco) = R$30,00.
Atenção: Para você voltar ao post: Pegadinhas em Questões de Lógica Matemática nos Concursos Públicos, Clique Aqui!
Atenção: Para você voltar ao post: Pegadinhas em Questões de Lógica Matemática nos Concursos Públicos, Clique Aqui!
 |
| A Matemática Aqui é Simples e Descomplicada! |







Assunto muito bem abordado.
ResponderExcluirParabéns!
Obrigado caro leitor(a).
ExcluirSe gostou divulgue e aproveite outros conteúdos do blog também.
Um abraço!
sou matematico e amei tdas elas so reparei um pequeno erro na ultima questão mas mesmo assim ta ótimo.
ResponderExcluirCaro colega, obrigado pela visita e pelos elogios ao nosso modesto blog.
ExcluirNão conseguimos visualizar o erro que você mencionou. Se puder nos informar, ficaremos agradecidos e claro que retificaremos!
Estamos sempre aprendendo também. Um grande abraço!
Gostei bastante das postagens , estou utilizando as questões no EJA .. Obrigado.
ResponderExcluirBom dia caro leitor, Brunosex!
ExcluirAgradecemos sua visita ao blog e ficamos felizes em saber que está aproveitando nossos conteúdos. Gostaríamos de convidá-lo a ser nosso seguidor no blog, assim como os demais leitores e nunca perderem novos conteúdos que são publicados periodicamente. Qualquer dúvida, conte conosco. Um grande abraço!
A resposta da questão 8 e 9 não me convenceu, achei sucinta a explicação.
ResponderExcluirBom dia!
ExcluirPrimeiramente agradecemos sua visita e participação ao nosso site.
Quanto a resposta da questão 8. É uma sequência simples, em que cada termo é o anterior menos os seguintes números, ou seja: Complete a sequência corretamente: 29,28,26,23,19;... Resp. 14. Observe que cada termo, a partir do 1º é o anterior -1, -2, -3, -4, -5 ... logo: 29, 29-1, 28-2, 26-3, 23-4, 19-5, ou 19-5=14. Na questão 9 é o mesmo raciocínio: 88,84,76,60;...
Resposta: 28, Agora devemos subtrair (ou somar) ao termo anterior: -4,-8,-16 e atual -32 → 60-32=28.
Caso não tenha entendido, entre em contato novamente. Obrigado!
Nossa!!! Essas pegadinhas matemática são ótimas. Parabéns!!
ResponderExcluirNossa!!! Essas pegadinhas matemática são ótimas. Parabéns!!
ResponderExcluirBom dia Edina!
ExcluirPrimeiramente agradecemos sua visita e também seu comentário sobre nosso artigo. São leitores como você que nos incentivam em nosso propósito de divulgar conhecimentos. Muito obrigado!
Grande abraço a todos!
Boa Noite Caro leitor.
ResponderExcluirDesculpe nossa falha na explicação da questão 1, deveria constar: 132,00 = 110,00 + 110,00x0,20 para entender que: 132,00 = 110,00 + 22,00. Agradecemos a observação e estamos retificando essa falha na solução. Se ainda assim persistir sua dúvida, retorne com novo comentário. Grande abraço!