Cálculo - Regra de L'Hospital
Para entendermos corretamente este conteúdo do Cálculo, chamado de Regra de L'Hospital ou simplesmente Regra de L'Hôpital, o qual consiste numa regra prática para resolver alguns tipos de limites que apresentam as indeterminações abaixo relatadas, é necessário que você tenha conhecimento prévio das derivadas, e que domine todas as regras de derivação que já foram estudadas neste site. Caso não tenha conhecimento do assunto, recomendamos veementemente acessar e se inteirar de nosso post chamado: Derivadas!, onde, você vai encontrar a definição e saber muito mais e tudo com maiores detalhes. Esclarecemos que geometricamente, ela é vista como a inclinação de uma curva e ainda que fisicamente, uma derivada pode ser interpretada, como uma taxa de variação, mas o assunto não será aqui abordado, tendo em vista que ele já foi por nós estudado naquela ocasião.
Aconselhamos também acessar nosso post chamado Limites!, para estudar e se inteirar do assunto Limites, que é de grande importância na Matemática e de outras áreas das exatas e conhecer as suas aplicações matemáticas e também nas demais ciências.
Mas, se você perceber, muitas vezes nos deparamos com certos tipos de limites, que embora usando todas as regras de derivação e mesmo fatorando suas funções envolvidas, não conseguimos achar uma solução real. Foi aí então que surgiu a regra de L'Hospital, que também foi chamada de regra de Cauchy, e que foi incorporada no primeiro livro de texto sobre Cálculo Diferencial, publicado por Guillaume François Antoine, Marquês de L'Hôpital, em 1712, para nos ajudar a encontrar as devidas soluções para certos tipos de limites, com soluções iniciais tidas como indeterminadas. Enfatizamos, no entanto, que foi o matemático Bernoulli, embora a publicação tenha sido creditada a L'Hospital, o qual emprestou seu nome ao feito, por descobrir uma propriedade que nos permite calcular rapidamente limites com esses tipos de indeterminações.
Esta intrigante descoberta consiste em perceber que, na vizinhança de um ponto, podemos comparar o quociente de duas funções, com o quociente de suas derivadas, desde que determinadas hipóteses sejam satisfeitas.
Mas, se você perceber, muitas vezes nos deparamos com certos tipos de limites, que embora usando todas as regras de derivação e mesmo fatorando suas funções envolvidas, não conseguimos achar uma solução real. Foi aí então que surgiu a regra de L'Hospital, que também foi chamada de regra de Cauchy, e que foi incorporada no primeiro livro de texto sobre Cálculo Diferencial, publicado por Guillaume François Antoine, Marquês de L'Hôpital, em 1712, para nos ajudar a encontrar as devidas soluções para certos tipos de limites, com soluções iniciais tidas como indeterminadas. Enfatizamos, no entanto, que foi o matemático Bernoulli, embora a publicação tenha sido creditada a L'Hospital, o qual emprestou seu nome ao feito, por descobrir uma propriedade que nos permite calcular rapidamente limites com esses tipos de indeterminações.
Esta intrigante descoberta consiste em perceber que, na vizinhança de um ponto, podemos comparar o quociente de duas funções, com o quociente de suas derivadas, desde que determinadas hipóteses sejam satisfeitas.
Resumindo, usamos a regra de L'Hospital para resolver certos tipos de limites, quando por substituição direta, tais limites apresentarem como resultado, as indeterminações do tipos (0/0) ou (¥/¥).
Então, dizemos que:
a) Primeira Regra de L'Hospital.
Sejam f e g duas funções contínuas num intervalo I, deriváveis no interior de I, tais que 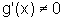 para todo x no interior de I. Seja
para todo x no interior de I. Seja 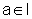 e suponhamos que
e suponhamos que 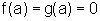 e que existe
e que existe 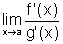 , finito ou infinito. Então existe
, finito ou infinito. Então existe 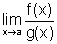 e mais ainda
e mais ainda 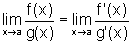 .
.
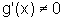 para todo x no interior de I. Seja
para todo x no interior de I. Seja 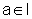 e suponhamos que
e suponhamos que 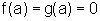 e que existe
e que existe 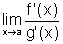 , finito ou infinito. Então existe
, finito ou infinito. Então existe 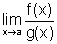 e mais ainda
e mais ainda 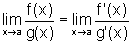 .
.
b) Segunda Regra de L'Hospital.
Sejam f e g duas funções deriváveis em todo ponto x distinto de a, x pertencente a uma vizinhança V de a, 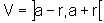 , r>0. Suponhamos que
, r>0. Suponhamos que 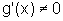 para todo
para todo 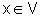 e que
e que 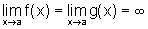 . Se existe
. Se existe 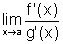 , finito ou infinito, então existe
, finito ou infinito, então existe 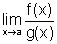 e, mais ainda,
e, mais ainda, 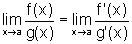 .
.
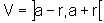 , r>0. Suponhamos que
, r>0. Suponhamos que 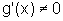 para todo
para todo 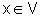 e que
e que 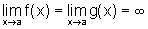 . Se existe
. Se existe 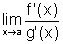 , finito ou infinito, então existe
, finito ou infinito, então existe 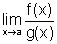 e, mais ainda,
e, mais ainda, 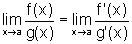 .
.
Em termos práticos, esta regra consiste que derivemos as funções f e g, até que encontremos um resultado real e satisfatório, que seja alcançado por substituição na respectiva variável das funções envolvidas, mas é preciso ter muito cuidado para verificar se as hipóteses estão sempre satisfeitas..
Nota: Caso encontremos como resultado, qualquer outras indeterminações, devemos usar de certos artifícios matematicamente aceitos, até fazer com que estas, se enquadrem nos dois tipos de indeterminações acima mencionados, para que a regra seja aplicada e seu resultado esteja correto.
Exemplos:
1) Lim(x→1) x² -1 / x-1
Solução: Notemos que substituindo a variável x por 1, temos: 1²-1 / 1-1 ou 0/0, que é uma indeterminação. Então, apliquemos a regra de L'Hospital, derivando as funções do exercício, então:
Lim(x→1) x² -1 / x-1 = Lim(x→1) 2x -0 / 1-0 = Lim(x→1) 2x
Agora, substituindo x por 1, temos o resultado: Lim(x→1) 2x = 2.1 = 2
Uma outra maneira de se resolver, seria usando da fatoração:
Lim(x→1) x² - 1 / x-1 = Lim(x→1) (x-1)(x+1) / x-1= Lim(x→1) x+1 = 1+1 =2
Mas, nem sempre o artificio se torna possível, portanto aconselhamos sempre usar a regra de L'Hospital, para casos onde não podemos fatorar.
2) Lim (x→1) lnx / x-1
Substituindo x por 1 diretamente na expressão, temos:
ln1 / 1-1 = 0/0 (indeterminação)
Aplicando a regra estudada e derivando-se, temos:
Lim(x→1) lnx / x-1 = Lim(x→1) 1/x / 1 = Lim(x→1) 1/x
Agora, substituindo x por 1, temos: 1/1 = 1
Solução: Substituindo diretamente o x por 2, teremos:
Lim(x→2) x² + 2x - 8 / x² -x -2 = 2² + 2.2 - 8 / 2² - 2 - 2 = 0/0 (indeterminação)
Vamos derivar ambas as funções da expressão, então:
Lim(x→2) x² + 2x - 8 / x² - x - 2 = Lim(x→2) 2x + 2 / 2x - 1
Substituindo x por 2, teremos: 2.2 + 2 / 2.2 - 1 = 6/3 = 2
4) Lim(x→0) e^x - x - 1 / x²
Solução: Substituindo x por zero diretamente, teremos:
Conclusão:
e>0 - 0 - 1 / 0>2 = 0/0 (indeterminação)
Então, devemos derivar:
Lim(x→0) e^x - x - 1 / x² = Lim(x→0) e^x - 1 - 0 / 2x
→ Lim(x→0) e^x - 1 / 2x, Note que substituindo o x por zero novamente, temos: e>0 - 1 / 0 = 1 - 1 / 0 = 0/0 (novamente a indeterminação).
Então, derivamos novamente e teremos:
Lim(x→0) e^x - 1 / 2x = Lim(x→0) e^x - 0 / 2 = Lim(x→0) e>x / 2
Agora, substituindo o x por zero, teremos: e>0 / 2 = 1/2
5) Lim (x→1) 1 - x + lnx / x³ - 3x + 2
Solução: Subst. diretamente o x por 1, teremos: 1 - 1 + ln1 / 1³ - 3 +2
= 1 - 1 + 0 / 1 - 3 + 2 = 0/0 (indeterminação),
Então, devemos derivar:
Lim (x→1) 1 - x + lnx / x³ - 3x + 2 = Lim (x→1) (0 - 1 + 1/x) / 3x² - 3 +0 = Lim(x→1) -1 +1/x / 3x² -3
Substituindo diretamente o x por 1, temos: (-1+1/1) / 3 - 3 = 0/0 (indeterminação),
Devemos derivar novamente, então:
(Note que 1/x = x>-1) → Lim(x→1) -1 + 1/x / 3x² -3 = Lim(x→1) -1 + x>-1 / 3x² -3
Quando derivamos temos que: Lim(x→1) -1 + x>-1 / 3x² -3
= Lim(x→1) 0 - x^-2 / 6x - 0 = Lim(x→1) -x>-2 / 6x = Lim (x→1) (-1/x²) / 6x
E, substituindo o x por 1, temos:
-1/1² / 6.1 = -1/6
6) Lim (x→0) x.lnx
Quando substituímos x por 0 temos: 0.ln0 = 0(-¥)= indeterminação.
Então, para usarmos L'Hospital, temos que transformar tal indeterminação em (0/0) ou em (¥/¥).
Então, usamos o seguinte artificio: Lim (x→0) x.lnx = Lim (x→0) (x/1).lnx
= Lim (x→0) lnx/1 ÷ 1/x → (subst.x por o) → ln0/1 ÷ 1/0 = indeterminação:(¥/¥).
Usando então a regra estudada, vamos derivar:
Lim (x→0) lnx / x^-1 = Lim (x→0) 1/x / -1x^-2 = Lim (x→0) 1/x / -1/x²
= Lim (x→0) 1/x . (-x²) = Lim (x→0) -x = -0 = 0
Então, devemos derivar:
Lim(x→0) e^x - x - 1 / x² = Lim(x→0) e^x - 1 - 0 / 2x
→ Lim(x→0) e^x - 1 / 2x, Note que substituindo o x por zero novamente, temos: e>0 - 1 / 0 = 1 - 1 / 0 = 0/0 (novamente a indeterminação).
Então, derivamos novamente e teremos:
Lim(x→0) e^x - 1 / 2x = Lim(x→0) e^x - 0 / 2 = Lim(x→0) e>x / 2
Agora, substituindo o x por zero, teremos: e>0 / 2 = 1/2
5) Lim (x→1) 1 - x + lnx / x³ - 3x + 2
Solução: Subst. diretamente o x por 1, teremos: 1 - 1 + ln1 / 1³ - 3 +2
= 1 - 1 + 0 / 1 - 3 + 2 = 0/0 (indeterminação),
Então, devemos derivar:
Lim (x→1) 1 - x + lnx / x³ - 3x + 2 = Lim (x→1) (0 - 1 + 1/x) / 3x² - 3 +0 = Lim(x→1) -1 +1/x / 3x² -3
Substituindo diretamente o x por 1, temos: (-1+1/1) / 3 - 3 = 0/0 (indeterminação),
Devemos derivar novamente, então:
(Note que 1/x = x>-1) → Lim(x→1) -1 + 1/x / 3x² -3 = Lim(x→1) -1 + x>-1 / 3x² -3
Quando derivamos temos que: Lim(x→1) -1 + x>-1 / 3x² -3
= Lim(x→1) 0 - x^-2 / 6x - 0 = Lim(x→1) -x>-2 / 6x = Lim (x→1) (-1/x²) / 6x
E, substituindo o x por 1, temos:
-1/1² / 6.1 = -1/6
6) Lim (x→0) x.lnx
Quando substituímos x por 0 temos: 0.ln0 = 0(-¥)= indeterminação.
Então, para usarmos L'Hospital, temos que transformar tal indeterminação em (0/0) ou em (¥/¥).
Então, usamos o seguinte artificio: Lim (x→0) x.lnx = Lim (x→0) (x/1).lnx
= Lim (x→0) lnx/1 ÷ 1/x → (subst.x por o) → ln0/1 ÷ 1/0 = indeterminação:(¥/¥).
Usando então a regra estudada, vamos derivar:
Lim (x→0) lnx / x^-1 = Lim (x→0) 1/x / -1x^-2 = Lim (x→0) 1/x / -1/x²
= Lim (x→0) 1/x . (-x²) = Lim (x→0) -x = -0 = 0
7) Lim(x→¥) e^x / x²
Solução: Quando substituímos x por infinito diretamente na expressão, encontramos a indeterminação ¥/¥
Então, vamos derivar ambas funções:
Lim(x→¥) e^x / x² = Lim(x→¥) e^x / 2x (note que derivada de e>x = e>x)
Substituindo x por infinito, novamente encontramos ¥/¥
Então, devemos derivar novamente as funções expressas acima, então:
Solução: Quando substituímos x por infinito diretamente na expressão, encontramos a indeterminação ¥/¥
Então, vamos derivar ambas funções:
Lim(x→¥) e^x / x² = Lim(x→¥) e^x / 2x (note que derivada de e>x = e>x)
Substituindo x por infinito, novamente encontramos ¥/¥
Então, devemos derivar novamente as funções expressas acima, então:
Lim(x→¥) e^x / 2x = Lim(x→¥) e^x / 2 →(substituindo x por infinito)
Encontramos: e>¥ / 2 = ¥
8) Lim(x→¥) x² / e>x
Solução: Quando substituímos x por ¥, encontramos: (¥>2) / e>¥) que equivale a indeterminação: (¥/¥).
Apliquemos então, a regra estudada e, derivando-se a expressão, teremos:
Lim(x→¥) x² / e>x = Lim (x→¥) 2x / e>x = novamente achamos a indeterminação: (¥/¥).
Vamos derivar novamente, então:
Lim (x→¥) 2x / e>x = Lim (x→¥) 2 / e>x →
então, (substituindo x por ¥)→ 2 / e^¥= 2/¥= 0
-----------------------------------------------------------------------------------------------------
então, (substituindo x por ¥)→ 2 / e^¥= 2/¥= 0
-----------------------------------------------------------------------------------------------------
Solução das questões apresentadas no post: Valor Absoluto: Saiba como Demonstrar
1. │5x - 7│= 13.
De acordo com a definição de valor absoluto, 5x - 7 = 13 ou 5x - 7 = -13;
i) Se 5x - 7 = 13 → 5x = 13+7 → 5x = 20 → x = 20/5 → x = 4
ii) Se 5x - 7 = -13 → 5x = -13+7 → 5x = -6 → x = -6/5
Concluímos então que a equação tem as seguintes soluções: x = 4 ou x = -6/5.
2.│2x - 1│= │3 - 4x│
Novamente, pela definição, temos duas possibilidades:
i) 2x - 1 = 3 - 4x → 2x + 4x = 3 + 1 → 6x = 4 → x = 4/6 (÷2)→ x= 2/3;
ii) 2x - 1 = -(3 - 4x) → 2x - 1 = -3 + 4x → 2x - 4x = -3 + 1 → -2x = -2 (-1)→ 2x = 2 → x = 2/2 → x = 1
Logo, a equação acima, tem as seguintes soluções: x = 2/3 ou x =1.
3.│x - 5│= 1 - 2x
Agora, devemos observar a condição que o valor absoluto nunca deve ser negativo, portanto 1 - 2x >= 0 → -2x >= -1 (-1) → 2x <= 1 → x <= 1/2 (condição)
Usando novamente a definição de valor absoluto:
i) x - 5 = 1 - 2x → x + 2x = 1 + 5 → 3x = 6 → x = 6/3 → x = 2 (não serve, pois sabemos que x<=1/2)
ii) x - 5 = -(1-2x) → x - 5 = -1 + 2x → x - 2x = -1 + 5 → -x = 4 (-1) → x = -4 (serve, pois x= -4 <= 1/2)
Então, solução da equação acima é x = -4
4. │2x - 6│ = 6 - 2x
Notemos que a expressão entre barras, só difere da segunda pelo sinal, de sorte que a equação pode ser escrita como:
│2x - 6│ = -(6 - 2x)
Como │y│= -y ↔ y <= 0, → y = -(6 -2x) → y = 2x - 6
Então: │2x - 6│ = -(2x - 6) ↔ 2x - 6 <= 0
Mas, 2x - 6 <= 0 ↔ x <= 3, que é o conjunto solução da equação
---------------------------------------------------------------------------------------------------------------------------------------------1. │5x - 7│= 13.
De acordo com a definição de valor absoluto, 5x - 7 = 13 ou 5x - 7 = -13;
i) Se 5x - 7 = 13 → 5x = 13+7 → 5x = 20 → x = 20/5 → x = 4
ii) Se 5x - 7 = -13 → 5x = -13+7 → 5x = -6 → x = -6/5
Concluímos então que a equação tem as seguintes soluções: x = 4 ou x = -6/5.
2.│2x - 1│= │3 - 4x│
Novamente, pela definição, temos duas possibilidades:
i) 2x - 1 = 3 - 4x → 2x + 4x = 3 + 1 → 6x = 4 → x = 4/6 (÷2)→ x= 2/3;
ii) 2x - 1 = -(3 - 4x) → 2x - 1 = -3 + 4x → 2x - 4x = -3 + 1 → -2x = -2 (-1)→ 2x = 2 → x = 2/2 → x = 1
Logo, a equação acima, tem as seguintes soluções: x = 2/3 ou x =1.
3.│x - 5│= 1 - 2x
Agora, devemos observar a condição que o valor absoluto nunca deve ser negativo, portanto 1 - 2x >= 0 → -2x >= -1 (-1) → 2x <= 1 → x <= 1/2 (condição)
Usando novamente a definição de valor absoluto:
i) x - 5 = 1 - 2x → x + 2x = 1 + 5 → 3x = 6 → x = 6/3 → x = 2 (não serve, pois sabemos que x<=1/2)
ii) x - 5 = -(1-2x) → x - 5 = -1 + 2x → x - 2x = -1 + 5 → -x = 4 (-1) → x = -4 (serve, pois x= -4 <= 1/2)
Então, solução da equação acima é x = -4
4. │2x - 6│ = 6 - 2x
Notemos que a expressão entre barras, só difere da segunda pelo sinal, de sorte que a equação pode ser escrita como:
│2x - 6│ = -(6 - 2x)
Como │y│= -y ↔ y <= 0, → y = -(6 -2x) → y = 2x - 6
Então: │2x - 6│ = -(2x - 6) ↔ 2x - 6 <= 0
Mas, 2x - 6 <= 0 ↔ x <= 3, que é o conjunto solução da equação
Conclusão:
Este conteúdo está diretamente vinculado com os nossos estudos iniciais já abordados em nosso site, em derivadas, limites e continuidade que, aconselhamos que você acesse nosso marcador chamado Ensino Superior, para se inteirar das regras pertinentes de derivações e também entenda do que se trata limites e continuidade. Lá vocês vão encontrar, além da parte teórica, muitos exercícios sobre o assunto com detalhes. Aconselhamos também estudar em seu livro ou apostila o tema, inclusive realizando o máximo possível de questões para fixar a matéria abordada. Ainda assim, se persistirem dúvidas, pode deixar seu comentário abaixo, que responderemos rapidamente e assim que possível.
Se você quiser compartilhar a matéria com seus amigos, para que eles também se inteirem da regra estudada, compartilhe usando os atalhos para as redes sociais, logo ao final do post ou envie o endereço do blog aos mesmos. E, para criticar, elogiar, retificar ou acrescentar, use também o espaço para comentários, logo abaixo. Desde já, agrademos sua visita e parecer ao blog. Muito Obrigado!
 |
| A Matemática Aqui é Simples e Descomplicada! |




Comentários
Postar um comentário
Ficou alguma dúvida sobre a postagem acima ou quer deixar uma sugestão?
Escreva seu comentário no espaço apropriado, seja para elogiar, criticar ou expor dúvidas, que publicaremos e responderemos o mais rápido possível.
Atenção: Serão excluídos os comentários contendo propagandas e também aqueles que faltem com o respeito e educação a qualquer usuário do Blog ou, os que venham induzir nosso leitor a acessar conteúdos impróprios e eticamente não recomendados. Desde já, agradecemos sua participação!